連載「プロジェクションマッピング技術の変遷」、前回は、プロジェクタ画素毎の色補償についてご紹介しました。この技術によって、模様のついた投影面でも所望の見えを表示することが原理的に可能になるはずですが、実は多くのケースで、正しい色を再現できません。その要因として、(1) ある点に投影された画素の反射光が、投影面上の別の点を照射してしまう相互反射、(2) プロジェクタのピントが合っていない焦点ボケ、そして、(3) 投影された画素の光が投影面内部で散乱する表面化散乱の3つが主要なものとして挙げられます。これらが生じると、対象面上の各点において、同時に複数の画素がその明るさ・色に影響を与えることになります。これにより、画素独立に所望の色を再現することを暗黙の前提としていた色補償技術が正しく働かなくなります。
プロジェクションマッピングでは、これら複雑な光学現象を記述する計算モデルを考え、その逆問題を解くことで、表示したい色の再現を目指すことになります。今回はまず、相互反射と焦点ボケ、それぞれの問題を解決する技術についてご紹介します。
目次
１ 相互反射補償
２ 焦点ボケ補償
２．１ 複数台投影アプローチ
２．２ 1台投影アプローチ
２．３ 投影光学系の工夫による１台投影における技術的限界の解消
３．まとめ
謝辞
参考文献
１ 相互反射補償
現実世界で、凹形状の面（面同士が向かい合っている）に光が照射すると、一方の面での反射光が他方の面に照射し、その反射光がまたもとの面に照射し、というように、反射が繰り返されます。コンピュータグラフィクスでは、この相互反射を考慮したレンダリング技法を利用することで、生成画像のリアリティを向上させています。図1は、相互反射を考慮せずにレンダリングしたものと、考慮したものとを示しています。相互反射によって、面と面が向かい合っている箇所（例えば、壁と小箱の側面）では、互いの面の反射光の影響を受けて明るくなり、色のついた左右の壁から反射された光によって小箱の側面が色づく様子を再現することができます。
プロジェクションマッピングでも同様に、凹面や、面同士が向かい合っているところでは、相互反射が発生します。前回ご紹介した色補償技術は、プロジェクタの各画素が照射する面の色は、他の画素の影響を受けないことを前提にしていました（1対1対応）。しかしながら、相互反射が生じるケースでは、1対多対応となりこの前提が成り立たなくなりますので、所望の見えを再現することができなくなります。具体的には、凹面だけ所望の見えよりも明るくなってしまいます（図2）。そこで、コンピュータグラフィクスで相互反射を計算する際に用いられるラジオシティ法の逆問題を解くことで、その影響を補償する手法が提案されています [1,2]。ここでは、数学的にも明解な[1]の手法をご紹介します。
前回と同様の考え方で、問題を定式化していきます。対象は拡散反射面とし、プロジェクタの出力特性は線形化されているものと仮定します。まず、相互反射が生じていない状況を考えます。ラジオシティ法では、対象面をパッチと呼ばれる小領域に分割して計算を進めます。対象面上のあるパッチ\(\mathit{i}\)に着目したとき、プロジェクタへの入力画素値を\(p_{i} \)、対象までの距離や入射角を考慮した減衰項を\(f_i%0\) 、パッチ\(\mathit{i}\)の反射率を\(r_{i}\)、カメラで観測した反射光の放射輝度を\(c_{i} \)とすると、これらの関係は、前回の定式化をそのまま用いて、以下のように表されます（図3）。
\(c_{i}=r_{i} f_{i} p_{i}\)
なお、環境光による影響\( e_{i}\)は、簡単のため今回の定式化では含めていません。また、拡散反射面では、放射輝度\(c_{i} \)の反射光がカメラ方向だけでなく全方位に広がります。
次に、相互反射が生じる状況を考えます。パッチ間での相互反射を考慮して、放射輝度を更新します。パッチ間での光のやり取りを算出するために、フォームファクタを計算します。フォームファクタ\(F_{i j}\)は、パッチ\(\mathit{i}\)が放射するエネルギーのうちパッチ\(\mathit{j}\)が受け取る割合を示し、図4のように\(\mathit{i}\)-\(\mathit{j}\)間の距離\(l_{i j}\)、\(\mathit{i}\)-\(\mathit{j}\)間を結ぶベクトルとパッチ\(\mathit{i}\),\(\mathit{j}\)のそれぞれの法線ベクトルがなす角 \( \phi_{i} \) , \( \phi_{j} \) 、\(\mathit{i}\)と\(\mathit{j}\)それぞれの面積 \( A_{i}\) , \( A_{j}\) 、パッチ間を遮る遮蔽物がある場合に0、ない場合に1をとる係数 \( H_{i j}\)から、以下のように計算されます。
\(F_{i j}=\frac{1}{\pi} \int_{A_{i}} \int_{A_{j}} H_{i j} \frac{\cos \phi_{i} \cos \phi_{j}}{l_{i j}^{2}} d A_{j} d A_{i}\)
フォームファクタは投影対象面の幾何形状のみから算出でき、投影画像や対象の反射率に依存しません。このため、プロジェクタと対象との位置姿勢関係が変わらない限り、あらかじめオフライン処理で計算しておけば良いことになります。以上より、ラジオシティ法に基づいて、相互反射を考慮した各パッチの放射輝度は以下の式でモデル化することができます。
\(c_{i}=r_{i} f_{i} p_{i}+r_{i} \sum_{j} F_{j i} c_{j}\)
今、目標輝度値を\(c_{i}^{t}\)と設定したとき、それを表示するためのプロジェクタへの入力画素値 \( \tilde{p}_{i} \) は、この式を以下のように変形することで求めることができます。
$$ \tilde{p}_{i}=\frac{c_{i}^{t}-r_{i} \sum_{j} F_{j i} c_{j}^{t}}{r_{i} f_{i}} $$
[1]では、未知数である反射率\(r_{i}\)は対象面全体に均一で1.0（おそらく）と仮定されています。もう一つの未知数\( f_{i}\)は、理論的には投影距離やプロジェクタの最大輝度に関わる項\( f_{i}^{1} \)と、入射角\( \theta_{i} \)に関わる項\( f_{i}^{2}=\cos \theta_{i} \)の積（つまり、\(f_{i}=f_{i}^{1} f_{i}^{2}\)）で表されます。[1]では、投影距離を固定とし\(f_{i}^{1}\)を予め較正することで、\(f_{i}\)を入射角にのみ依存するものと仮定しています。また、投影対象内での投影距離の差は、対象全体とプロジェクタとの距離に比べて相対的に小さいため無視できる（つまり、\(f_{i}^{1}\)は投影面内で一定）と暗黙的に仮定しています。このように書くと、かなり仮定が多く、制約の多い手法のように感じられるかもしれません。とはいえ、この手法は解析的に相互反射を補償する映像投影を可能にする強力なツールです。プロジェクションマッピングからは少し離れてしまいますが、巨大な凹面形状の投影スクリーンでユーザーを覆い隠すCAVEのような没入型VRシステムでの活躍が期待できます。なお、上述の仮定を考慮する必要のない手法については、本連載の次回にご紹介したいと思います。
では、相互反射補償の例として、[2]の論文中に示されている投影結果を確認してみましょう。図5の左側が相互反射補償せずに投影したもので、右側が相互反射補償を適用した結果です。相互反射補償のない場合は、投影対象コーナー部分に不自然に明るい領域が生じていますが、相互反射補償を適用することで、その影響が抑えられていることが確認できます。
２ 焦点ボケ補償
プロジェクタのピントが合っていないと、焦点ボケにより映像がぼやけます。ピントがあっている状態のことを合焦と呼び、レンズから合焦している地点までの距離を合焦距離と呼びます。レンズからの距離が合焦距離と異なる場合、投影画素は大きくなり（焦点ボケ）近傍の画素同士が重なり合います。これによって、投影面上の各地点には、複数の画素が重なり合って照射することになります。プロジェクタは一般的に、高い輝度を確保するためレンズ開口（絞り）が広く設計されています。このため、被写界深度（焦点ボケの生じない範囲）は浅く、合焦地点から少し離れるだけで、すぐに映像がボケてしまいます（レンズ開口と被写界深度の関係については、他の専門文献をご参照ください）。このため、単一平面だけに限らない対象に映像投影することが前提となるプロジェクションマッピングでは、ほとんどのケースで焦点ボケが生じてしまいます。その解決方法として、2つのアプローチが研究されています。
２．１ 複数台投影アプローチ
異なる地点に合焦するように合焦距離を設定した複数台のプロジェクタで、焦点ボケの生じないように補い合うアプローチが提案されています [3]。原理はシンプルです。まず、異なる合焦地点を設定した各プロジェクタから、ドットパターンを投影します。次に、投影対象の各小領域で、投影されたドットの大きさをプロジェクタ間で比較して、最も小さいドットを投影しているプロジェクタを割り当てます（図6）。ドットの観測には、投影対象全体が被写界深度内に入るような開口の小さいカメラを用います（露光時間を長くすれば、ドットは観測可能です）。そして、割り当てられたプロジェクタから各領域に映像投影することで、焦点ボケの少ない映像投影が可能となります。
図7に投影結果を示します。2台のプロジェクタを用いて、円柱のような形状の対象に投影した結果です。1台目のプロジェクタの合焦距離を対象の奥側に、2台目の合焦距離を手前側に設定しています（同図右）。そして、上記の方法を用いて、対象の各領域でそこに投影すべきプロジェクタを選択し、投影画像を生成します（同図中）。投影結果を確認すると、2台目のプロジェクタのみで投影したものと比べて、この手法での投影結果では、投影画像全体に渡ってボケのない表示ができていることが確認できます（同図右）。この手法は、原理がシンプルで直観的にわかりやすいため、プロジェクタを複数用いることができる場合は、積極的に利用することをおすすめします。一方、プロジェクタが1台しか無いような場合には対応できません。
２．２ 1台投影アプローチ
プロジェクタからの投影画質が焦点ボケによって劣化している場合に、投影画像をソフトウェア補正することで、その劣化を補償する技術の研究が進められています。焦点ボケによる劣化は、画像処理における空間ローパスフィルタリングとみなすことができます。そこで、その逆フィルタを適用することで、焦点ボケを補償する、というのが基本的な考え方となります。
まず、問題を簡単化して、投影対象は平面でプロジェクタからの距離が全て同じであり、全ての投影光が投影面に垂直に入射し、さらに、面全体で均一な反射率 (=1.0) を持つと仮定します。また、相互反射のときと同様、簡単のため環境光の影響はないものと考えます。この場合、焦点ボケの程度は面上で全て同じになります。焦点ボケにより劣化した画像\(c(x,y)%0\)は、投影する入力画像\(p(x,y)%0\)および点拡がり関数 (Point Spread Function: PSF) \(h(x,y)%0 \) を用いて、以下の畳み込み計算 (convolution) により表されます（図8）。
\(c(x,y)=p(x,y)*h(x,y)%0\) ・・・式(1)
\(\ \ \ \ \ \ =\sum_u\sum_v p(x+u,y+v)h(u,v)%0\)
ここで、記号\(*%0\)は、畳み込み演算を表します。焦点ボケのPSFとして代表的なものとしては、ガウス分布が挙げられます。
\(h(x,y)=\frac{1}{2\pi\sigma^2}\exp(-\frac{x^2+y^2}{2\sigma^2})%0\)
今、焦点ボケ劣化後に目標画像\(c^t(x,y)%0\)を表示したい場合、入力画像\(\tilde{p}(x,y)%0\)は、式(1)の逆計算 (deconvolution) することで求められます（図8）。
\(\tilde{p}(x,y)=c^t(x,y)*h^{-1}(x,y)%0\)
畳み込み和はフーリエ変換すると積の計算となることから、ウィナーフィルタを採用してノイズの影響を抑えた最適な入力画像を求める方法が提案されています[4,5]。具体的には、 \( c(x,y)%0 \) 、 \( p(x,y)%0 \) 、 \( h(x,y)%0 \) のフーリエ変換をそれぞれ \( C(u,v)%0 \) 、 \( P(u,v)%0 \) 、 \( H(u,v)%0 \) として、以下のように求めます。
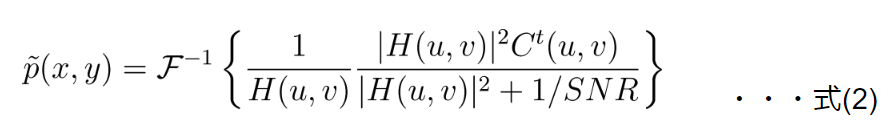
ここで\(\mathcal{F}^{-1}%0\)はフーリエ逆変換を、\(SNR%0\)は適当な信号雑音比を表します。
次に、実際のプロジェクションマッピングでの利用を想定し、これまでの理想的な仮定を緩めて、対象面が平面ではなく、プロジェクタからの距離が対象上で不均一になる状況を考えます。この状況では、焦点ボケ具合、つまり、PSFが画素ごとに異なります。式(2)に示すウィナーフィルタは画像全体に均一なPSFを仮定していますので、そのままでは解くことができません。この問題に対しては、まず対象面を似たようなPSFを持つ小領域に分割し、次にその各領域ではPSFは均一であると仮定してウィナーフィルタを適用し、小領域ごとに焦点ボケ補償画像を求め、最後にそれらをつなぎ合わせて投影画像を生成する、という方法が提案されています[4,5]。図9に、[4]の研究で示されている投影結果を示します。プロジェクタに対して斜めに置かれた平面に映像投影しています。原画像をそのまま投影した場合に比べて、焦点ボケ補償を適用した方が、原画像の高周波成分を残した投影結果となっていることが確認できます。
さらに、より現実のプロジェクションマッピングで想定される状況を考えてみたいと思います。つまり、面の反射率が空間的に異なり（つまり、模様があり）、入射角も面上で異なるとします。このとき、対象の反射率\(r(x,y)%0\)、および、入射角とプロジェクタからの距離に依存した減衰項\(f(x,y)%0\)を考慮する必要があるので、式(1)にそれらを加えると、
\(c(x,y)=r(x,y)f(x,y) (p(x,y)*h(x,y))%0\)
となります。この場合も、目標\(c^t(x,y)%0\)を表示するための入力画素値\(\tilde{p}(x,y)%0\)は、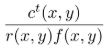
をフーリエ変換したものを\(C^t(u,v)%0\)とすることで、式(2)を用いて求めることができると考えられます。実はこのモデル、本当に適切に動くのかどうか、私自身を含め、まだ世界中の誰も試していないと思います（私の知る限り、ではありますが）。もし読者の方の中で、実験された（これからされる）方がいらっしゃいましたら、是非その結果を教えていただきたいと思います。
２．３ 投影光学系の工夫による１台投影における技術的限界の解消
2.2節でご紹介してきたウィナーフィルタを基盤とした手法には、大きく分けて２つの限界があります。まず、小領域分割は対象面がなだらかに形状変化していると仮定する場合はうまく働きますが、急激な変化がある場合には領域内のPSFが均一であるという仮定が成り立たなくなるため、適切に動作しない点が挙げられます。２つ目の限界として、ウィナーフィルタで計算された入力画像の画素値が、一般的なプロジェクタの輝度階調（8 bit、つまり、0から255の整数値）を外れてしまう可能性が挙げられます。外れた値は、無理やり0や255に丸めなければならなくなり、その誤差によって、投影結果にノイズが含まれる可能性があります。そこで、これら技術的限界を解消するアプローチとして、投影光学系を工夫する技術が提案されています。
１つ目の技術的限界は、PSFが空間的に変化することに起因したものでした。この問題に対して、我々の研究グループは、合焦距離を前後に高速振動（以降、フォーカルスイープと呼びます）させることで、見かけ上のPSFを、プロジェクタからの距離によらず一定とする技術を開発しました[6]。具体的には、電気式焦点可変レンズ (Electrically Focus-Tunable Lens: ETL) をプロジェクタのレンズとして用い、1秒間に60周期のスピードで合焦距離を振動させます。合焦距離の振動範囲は、対象面のプロジェクタに最も近い点から最も遠い点までをカバーするよう設定します。ETLには、大口径で応答性の高い液体式のものを利用しています。これは、液体を薄膜でサンドイッチした構造になっており、リング形状のアクチュエーターがその外側を抑え込むことで厚みが変わってレンズの屈折力（ひいては合焦距離）を変化させます。フォーカルスイープをゆっくり行うと、投影映像がボケたりくっきり見えたりと、合焦距離の変化を知覚することができます。一方、その周波数が60 Hzを超すと、パラパラ漫画の要領で人にはその変化が感知できなくなります。つまり、1/60秒間（1周期分）のPSFの変化は知覚されず、その足し合わされたものが見かけ上のPSFとなります。我々は、この見かけ上のPSFが、スイープ範囲内の対象面上で常にほぼ一定になることを数学的に示し、実験的に確認しました（図10）。つまり、プロジェクタからの距離が変わっても、PSFは変化しないという投影系を構築することに成功しました。これによって、原理的には、原画像に対して一つのPSFを用いてウィナーフィルタ（式(2)）を適用することで、焦点ボケ補償する投影画像を求めることができます。（実際はもう少し複雑な処理が必要ですが、文量の関係上割愛します。詳しくは[6]をご確認ください。）
図11に、ETLを取り付けたプロジェクタを用いて、距離が一定ではない対象面への投影結果を示します。この結果から、原画像をそのまま投影した場合と比べて、我々の提案するフォーカルスイープ投影と焦点ボケ補償を組み合せて適用した場合は、投影面全体に渡ってシャープな映像投影が可能となっていることが確認できます。また、図12に、投影面を動かしたときの投影結果を示します。提案手法を適用した場合は、投影面が移動しても常にシャープな映像が表示されていることが確認できます。2.1および2.2節で述べてきた手法では、投影シーンごとに対象面にドットパターンなどを投影してPSFを予め計測する必要があり、動物体への対応が困難でした。一方、我々の手法ではPSFは投影距離に依存せず一定なので、動物体にドットパターンを逐次投影する必要がなく、動的なプロジェクションマッピングでも利用可能です。
次に、２つ目の技術的限界ついて考えます。2.2節の最初でも述べたように、焦点ボケは、空間的なローパスフィルタとして機能しているため、PSFの高周波成分はほぼゼロとなります。そのため、式(2)の分母が高周波成分で非常に小さくなるため、計算される\(\tilde{p}%0\)の値が255を超えてしまう画素が高周波パターンとして現れてしまいます（リンギングとも呼ばれます）。これを解決する方法として、投影光のPSFを、高周波成分も通過させるようにする技術が提案されています[7]。具体的には、符号化開口 (coded aperture) という技術を用います。図13に示すように、投影光のPSFは、開口と同形（上下・左右反転）となります。つまり、小さな穴がランダムに空いているような符号化開口を採用すると、PSFに細かなパターンが現れ、高周波成分を多く含むことになります。これにより、式(2)の分母が高周波でもゼロより大きな値を持つこととなり、リンギングを抑制した焦点ボケ補償が可能となります。
[7]で示されている実験の結果を図14に示します。この図の通り、符号化開口を適用した方がリンギングが抑制されており、焦点ボケ補償の効果が高いことが示されています。興味深い考察としては、符号化開口を採用すると、プロジェクタ内部の光源から発せられる光の通過する総量は減ります。このため、このアプローチは、焦点ボケ補償の性能は向上しますが、投影結果の輝度は現象するというトレードオフを抱えています。
図14：一般的な円形の開口と符号化開口を用いた焦点ボケ補償結果の比較。左：原画像、中上：円形開口で原画像をそのまま投影、中右：円形開口で焦点ボケ補償画像を投影、下中：符号化開口で元画像をそのまま投影、下右；符号化開口で焦点ボケ補償画像を投影。（[7]より）３．まとめ
今回は、複数の投影画素が重なり合ってしまう状況をうみだす、複雑な光学現象を取り扱いました。特に、相互反射と焦点ボケに着目し、それらの影響を抑制して、所望の色を再現する技術についてご紹介しました。次回は、もう一つの光学現象である表面化散乱の影響を解消する技術にご紹介します。また、実は、相互反射・焦点ボケ・表面化散乱のすべての影響を、統一的に解消することができる枠組みがあります。次回は、「複雑な光学現象への対応（２）」として、こういった技術についてもご紹介できればと考えています。
謝辞
図8の作成には、大阪大学・大学院基礎工学研究科・博士前期課程在学の影山雄太さんにお手伝いいただきました。
参考文献
[1] 向川康博, 柿沼孝行, 大田友一, “非平面へのパターン投影のための相互反射の補償,” 情報処理学会論文誌：コンピュータビジョンとイメージメディア, Vol. 48, No. SIG1 (CVIM17), pp. 98-106, 2007.
[2] O. Bimber, A. Grundhofer, T. Zeidler, D. Danch and P. Kapakos, “Compensating Indirect Scattering for Immersive and Semi-Immersive Projection Displays,” In Proceedings of IEEE Virtual Reality Conference, pp. 151-158, 2006.
[3] O. Bimber and A. Emmerling, “Multifocal projection: a multiprojector technique for increasing focal depth,” IEEE Transactions on Visualization and Computer Graphics, Vol. 12, No. 4, pp. 658-667, 2006.
[4] M. S. Brown, P. Song, T. J. Cham, “Image Pre-conditioning for Out-of-Focus Projector Blur,” In Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1956-1963, 2006.
[5] 小山田 雄仁, 斎藤 英雄, “プロジェクタスクリーン上に生じる焦点ボケ解消のための投影画像の事前補正法,” バーチャルリアリティ学会論文誌, Vol. 12, No. 4, pp. 479-486, 2007.
[6] D. Iwai, S. Mihara, and K. Sato, “Extended Depth-of-Field Projector by Fast Focal Sweep Projection,” IEEE Transactions on Visualization and Computer Graphics, Vol. 21, No. 4, pp. 462-470, 2015.
[7] M. Grosse, G. Wetzstein, A. Grundhoefer and O. Bimber, “Coded Aperture Projection,” ACM Transactions on Graphics, Vol. 29, No. 3, Article No. 22, 2010.
#1「プロジェクションマッピング作品を通して見る技術課題」
１ 建築物へのプロジェクションマッピング
２ インタラクティブなプロジェクションマッピング
３ 動的プロジェクションマッピング
４ まとめ
#2「プロジェクションマッピングの多様なアプリケーション」
１ 照明の知能化
１．１ リビング照明の知能化
１．２ 作業空間の照明の知能化
２ 表面質感の編集
３ まとめ
#3 「幾何補正 (位置合わせ)」
１ 平面を対象とする場合の幾何補正
２ 立体面を対象とする場合の幾何補正
２．１ 対象面形状が既知の場合の較正
２．２ 対象面形状が未知の場合の較正
２．２．１ 事前プロカム較正アプローチ
２．２．２ 事前カメラ較正アプローチ
２．２．３ 自動較正アプローチ
３ まとめ
#4「色補償」
１ 準備
２ 簡易手法
３ 色変換行列手法
４ 非線形補間手法
５ ダイナミックレンジ制約の解消法
６ まとめ
#5「複雑な光学現象への対応（１）」
１ 相互反射補償
２ 焦点ボケ補償
２．１ 複数台投影アプローチ
２．２ 1台投影アプローチ
２．３ 投影光学系の工夫による１台投影における技術的限界の解消
３．まとめ
#6「 複雑な光学現象への対応（２）」
１ 表面化散乱補償
２ ライトトランスポート行列を用いた大域照明効果の一括補償
３ おわりに
#7「影の除去」
1 複数台のプロジェクタを用いた影除去
2 光学系の工夫による影除去
3 まとめ
#8「ハイダイナミックレンジ投影」
１ プロジェクタのダイナミックレンジ拡張
１．１ 単純に最大照度を上げてもダイナミックレンジは改善しない
１．２ 最小照度を下げてダイナミックレンジを拡げる技術
１．３ 最大照度向上と最小照度抑制によるダイナミックレンジ拡張技術
２ プロジェクションシステムのダイナミックレンジ拡張