[連載] プロジェクションマッピング技術の変遷 #3「幾何補正 (位置合わせ)」岩井大輔

執筆者：岩井 大輔　連載一覧

　連載「プロジェクションマッピング技術の変遷」ではこれまで、プロジェクションマッピング技術に関する総論的なお話が中心でしたが、今回より具体的なトピックを設定し、ご紹介していこうと思います。第3回目の今回は、ほぼあらゆるプロジェクションマッピングにおいて必要となる、幾何補正技術についてご紹介します。

　幾何補正とは、投影対象上の「所望の領域」に「所望の映像」を表示するための処理を指します。このように書くと一見、難解そうという印象を持たれるかもしれませんが、実は、私達がよく行っている作業も該当しています。それは、プレゼンテーションのためにスクリーンとプロジェクタを用意して、まず最初に行うこと、つまり、プロジェクタの位置・姿勢を調整して、投影領域をスクリーン上で矩形かつ望みのサイズにする作業のことです。プロジェクタに搭載されている台形補正機能を使えば、台形に歪んだ投影領域をソフトウェア的に矩形に調整することも可能です。このケースでは、「所望の領域」はスクリーン上の矩形であり、「所望の映像」はプレゼンテーションスライドということになります。

　スクリーンのような床に垂直な平面に投影する場合には、このように比較的単純な作業で幾何補正できます。一方、プロジェクションマッピングの多くのケースで想定されているような、曲面や複数の平面で構成される投影対象に、所望の映像を歪みなく表示する場合には、このような単純な方法では適切に幾何補正することはできません。つまり、投影対象の形状と投影コンテンツに依存して、適用すべき幾何補正は異なります。そこで、様々なケースに対して、どのような幾何補正アプローチを採るべきかをご紹介し、その背景にある原理についても簡単に解説したいと思います。

目次

１　平面を対象とする場合の幾何補正
２　立体面を対象とする場合の幾何補正
２．１　対象面形状が既知の場合の較正
２．２　対象面形状が未知の場合の較正
２．２．１　事前プロカム較正アプローチ
２．２．２　事前カメラ較正アプローチ
２．２．３　自動較正アプローチ
３　まとめ
参考文献

1　平面を対象とする場合の幾何補正

　幾何補正において最も単純なケースは、投影対象が平面の場合です。このとき、台形補正機能を用いることで簡単に幾何補正できるということは、先に述べたとおりです。しかしながら、台形補正が適切に働くのは、プロジェクタがスクリーンなどの対象平面に対し正対している状態から、ある一軸方向にだけ傾いている場合に限ります。これは例えば、机の上においたプロジェクタを少し上向きに傾けて設置するようなケースです。このとき、投影領域は台形に歪みますので、台形補正によってそれを矩形化することができます。

　一方、プロジェクタ設置の自由度を上げ、このプロジェクタをさらに左右方向に回転させると、対象平面上での投影領域は台形ではなくなります。この歪みを補正するためには、より高次の画像変形が必要となります。そこでここでは、平面を対象とする場合に、プロジェクタの位置・姿勢にかかわらず投影映像を矩形化する幾何補正技術 (ホモグラフィ変換) について紹介します (図1)。ホモグラフィ変換を用いた幾何補正の作業手順は次の通りです。

1. 対象平面で投影したい矩形領域を決めます
2. 指定した矩形領域を投影領域がカバーするようにプロジェクタを設置します
3. 矩形のコーナー点と対応するプロジェクタ画素を見つけます (本質的にはコーナー点である必要はなく、4点の対応関係が得られれば良いです)
4. 4点の対応関係を用いてホモグラフィ変換を行います

　ホモグラフィ変換とは、ある平面Aを射影変換を用いて別の平面aに変形する処理を指します。ここで平面A中のある点の座標を\((X,Y)%0\)とし、平面a中の対応する(変換後の)点の座標を\((x,y)%0\)とします。すると、この2点の関係は次のように表すことができます。

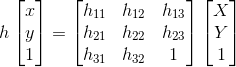
右辺の3×3の行列はホモグラフィ行列と呼ばれ、この中の8つの未知パラメータを適切に求めることができれば、平面A (対象平面上の矩形領域) からa (矩形ではないプロジェクタ投影領域) への変換を行うことができます。この変換は、2つの式へと展開できます。つまり、\((X,Y)%0\)と\((x,y)%0\)の対応が4つあれば8つの式が展開できますので、8つの未知パラメータを求めることができます。上記の手順3で、4点の対応関係が必要と書いた理由がここにあります。ホモグラフィ変換によって、対象平面の矩形領域の各点に対応するプロジェクタ投影領域の点が求められるので、投影映像を矩形化することができます。

　このようにホモグラフィ変換による幾何補正で必要なのは、4点の対応のみなので、簡単な手作業で動かすことができます。このため簡易なプロジェクションマッピングアプリには、この原理をベースに動いているものが多くあります (例：Optoma Projection Mapper)。また、プロジェクタ内蔵の機能として搭載されている例もあります (例：Epsonフレームフィット機能)。

2　立体面を対象とする場合の幾何補正

　投影対象が立体面になると、幾何補正のための作業は複雑になります。しかしながらプロジェクションマッピングにおいて立体面を対象とするケースは多くあります。ここではまず、予め何らかの方法で対象面の形状が計測済みである場合を考えます。このケースでは、形状データをUnityやUnreal Engineといった3DCG (3次元コンピュータグラフィクス) を作成するソフトで読み込んで、それらに映像を貼り付けることで投影コンテンツを作成するようなワークフローを想定しています。つまり、バーチャルな空間に現実空間と瓜二つのシーンを作成し、その面にプロジェクションマッピングで表現したい模様をつけます。このバーチャル空間から投影画像を生成して現実空間に投影します。

　投影画像は、現実空間のプロジェクタと同じ位置姿勢に設置したバーチャルなカメラでバーチャル空間を撮影することで生成します (図2)。このとき、プロジェクタの現実空間中での位置姿勢と、画角 (焦点距離) 等の情報が必要となるため較正が必要となります。なお、現実空間の「プロジェクタ」とバーチャル空間の「カメラ」とを同等に扱っていることに違和感のある方がいらっしゃるかもしれませんが、光学的に見ればプロジェクタとカメラはレンズを通る光の向きが逆なだけで、それ以外は同等なものです。つまり、外界の光がレンズを通って画像平面に結像するカメラと、画像平面から放出された光がレンズを通って外界で結像するプロジェクタとは、光学的に双対の関係にあります。このことから、現実空間でのプロジェクタの位置姿勢および画角等の較正には、カメラの較正技術を適用することができます。

　カメラ較正では、図3に示すように、現実空間中に規定された世界座標系に対して、カメラの光学中心を原点とするカメラ座標系の位置姿勢関係を表す外部パラメータ (回転行列\({\bf R}%0\)、並進ベクトル\({\bf t}%0)\)）と、カメラの内部パラメータ (焦点距離\((f_x, f_y)%0\)、光学的中心\((c_x, c_y)%0\)、せん断パラメータ\(s%0\)) を求めます。これらのパラメータを求めることで、以下の式によって、現実空間中の任意の3次元点 (世界座標系での位置\((X,Y,Z)%0\)) が、カメラ画像のどの画素 (カメラ画像座標系での位置\((x,y)%0)\) に写るのかを計算することができます。

\({\bf x}={\bf K}[{\bf R}|{\bf t}]{\bf X}%0\)

多くの場合、これらにレンズ歪みも考慮したモデルが利用されます。詳細については他の専門文献をご参照ください[1]。以降、このモデルの「カメラ」を「プロジェクタ」に置き換えて説明を進めます。

２．１　対象面形状が既知の場合の較正

　上のモデルの各パラメータを較正する方法は数多く提案されています。恐らく最も単純な方法は、世界座標系での3次元位置が既知である現実空間中の点と、そこに投影するプロジェクタ画素との対応を複数 (最低6対応) 取得するものです。3次元位置既知の点に対応するプロジェクタ画素は、例えばクリックしたら投影表示されたマウスポインタの画素位置を出力するようなソフトウェアを用いることで取得することができます。精度良く較正するには対応点数を増やせば良いのですが、手動で対応点を増やすのは手間がかかり現実的ではなく、プロジェクションマッピングのテストの際に利用するには良いかもしれませんが、実運用での利用はおすすめできません。

　プロジェクタは外界の情報を取得する術を持たないので、対応点取得を自動化するためには、外部のセンシング機器を用いる必要があります。そこで、カメラを用いてプロジェクションされた映像を観測するシステムがよく用いられます。このようなシステムのことを、プロカム系 (projector-camera system、略してprocams) と呼びます。プロカム系を用いて、自動的に現実空間中の点とプロジェクタ画素との対応を取得する方法として、空間コード投影法が広く用いられています。これは、プロジェクタの各画素の位置を何らかのパターンにコード化して投影する方法で、グレイコードと呼ばれるバイナリコードに座標値を変換する方法が特に良く用いられます (図4)。カメラで撮影された投影コードを座標値情報へとデコードすることで、カメラの各画素が撮影しているプロジェクタの各画素の座標値を得ることができます (camera-to-projector対応、略してC2P対応と呼びます)。つまり、3次元位置既知の点に画像マーカーを貼り付けておく等して、その点とカメラ画素との対応を自動取得できれば、カメラ画素を媒介してプロジェクタ画素との対応も得られるため、パラメータ較正することができます。

２．２　対象面形状が未知の場合の較正

　ここまで、予め対象面の形状が計測済みである場合を考えてきました。しかしながら、この仮定が成立しない場合も多くありそうです。そこで、プロジェクタのパラメータ較正を行いつつ、投影対象面の形状も計測する手法をご紹介します。形状計測が必要ということで、まず思い浮かぶアプローチとして、距離計測可能なカメラ (Microsoft KinectなどのRGB-Dカメラ) を用いることが考えられます。一旦、RGB-Dカメラで投影シーンの形状を計測してしまえば、先に述べた方法でプロジェクタを較正できます。RGB-Dカメラを用いるプロカム系の較正についてはMicrosoftよりソフトウェアツールが公開されています (RoomAlive Toolkit)。ただし、RGB-Dカメラは一般的に、遠方のものは計測範囲外となる等、利用シーンが限られます。そこで、そのような制約のない通常のカメラを用いたプロカム系での較正手法について紹介します。これには大きく分けて以下の3種類のアプローチがあります。

• カメラとプロジェクタを先に較正し、その後、投影対象面の形状計測を実施する事前プロカム較正アプローチ
• カメラを較正し、その後、プロジェクタ較正と形状計測を同時に実施する事前カメラ優先アプローチ
• 形状計測およびカメラ・プロジェクタの較正を同時に実施する自動較正アプローチ

それぞれ、利用シーンに合わせて使い分けることになります。

２．２．１　事前プロカム較正アプローチ

　まず、事前プロカム較正アプローチについてご紹介します。カメラの較正には、Zhangが提案したチェッカーボードを用いる較正手法が広く用いられています [2]。これは、チェッカーパタン (複数の黒と白のマス目) を印刷した平面の板を様々な位置姿勢で撮影し、それぞれのチェッカーのコーナー点のカメラ画像内での位置を計測することで、カメラの内部パラメータおよび外部パラメータ (撮影された平面のうちの1平面が世界座標系を定義) を求めるものです。既にOpenCV等の主要なプログラミングツールに関数が用意されているので、すぐに試すことができます。原理や技術的な詳細は原典や他の専門文献をご参照ください [1]。

　プロジェクタの較正でも同様に、各チェッカーコーナーのプロジェクタ画像内での位置を計測することで、Zhangの手法を用いることができます。コーナーに対応するプロジェクタ画素は、２．１で説明した空間コード投影法を用いることで求めることができます。空間コード投影法で利用するカメラ画像内でのチェッカーコーナーの位置が分かると、C2P対応からそのプロジェクタ内での位置が求まります。このとき、チェッカーボードの位置姿勢をカメラとプロジェクタの較正で同一にすると、同じ世界座標系での外部パラメータを求められます。なお、この手順でのプロカム系較正は、インターネット上で公開されているツールがあります (例えばこれとかです)。

　カメラとプロジェクタが較正できたら、投影シーンにプロジェクタからグレイコードパターンを投影してC2P対応を取得します。プロジェクタとカメラの双対性から、プロカム系は、カメラ２台のステレオカメラとみなすことができます。このため、C2P対応から三角測量の原理で対象までの距離が計測できるので、投影対象面を形状計測することができます。

２．２．２　事前カメラ較正アプローチ

　プロジェクタを較正するのには、チェッカーボードを異なる位置姿勢に設置するたびにグレイコードパターンを投影する必要があり時間がかかります。カメラが2台以上あれば、チェッカーボードを用いたプロジェクタ較正が不要になります。

　まず、チェッカーボードを用いてカメラを較正します。その後、プロジェクタからグレイコードパターンを投影シーンに投影し、C2P対応をカメラ毎に取得します。これにより、各プロジェクタ画素を観測しているカメラ画素を、カメラ毎に求めることができます。同一のプロジェクタ画素を観測しているカメラ画素の対の情報から、2台のカメラを用いた三角測量により、投影シーンの形状を求めることができます。形状が求まれば、２．１の方法を使ってプロジェクタの較正も行えます。

２．２．３　自動較正アプローチ

　事前のプロカム較正を行う必要なく、ある一つの枠組みで較正と投影シーンの形状計測を同時に達成することができれば、手間が少なく便利です。現在、このアプローチに関する研究が盛んに進められているところです [3,4]。基本的には、Structure from Motion (SfM) と呼ばれる、多視点画像から撮影シーンを3次元形状復元するコンピュータビジョンの技術がベースとなっています[5]が、いずれも研究段階であり、標準的な方法は未だ確立されていません。また、いずれも処理内容が複雑で、本連載の範囲を超えてしまっていますので、詳細説明は割愛させていただきます。なお、現在、最も性能が良い手法は[4]の論文が提案しているものですので、ご興味のある方は是非ご覧ください。今後、研究の進展に伴って、誰でも簡単に使えるツールの整備などが進むことと思います。

3　まとめ

　今回は、対象が非平面であっても、歪みなく映像を投影するための幾何補正技術についてご紹介しました。プロジェクションマッピングの利用状況に関わらず、「対象の形状計測」と「プロジェクタ較正」の2点が達成できれば、幾何補正が可能となります。今回の記事が、読者の方々が歪みのないプロジェクションマッピングを実現する一助になりましたら幸いです。なお、今回は投影対象が静止していることを前提にしていました。次回は、対象が動く場合の幾何補正技術についてご紹介する予定です。

次回：#4「色補償」

参考文献

1. 米谷竜, 斎藤英雄 (編著), “コンピュータビジョン―広がる要素技術と応用― ,” 未来へつなぐ デジタルシリーズ37, 共立出版, 2018.

2. Z. Zhang, “A flexible new technique for camera calibration,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 22, No. 11, pp. 1330-1334, 2000.

3. S. Yamazaki, M. Mochimaru and T. Kanade, “Simultaneous self-calibration of a projector and a camera using structured light,” In Proceedings of CVPR 2011 WORKSHOPS, pp. 60-67, 2011.

4. S. Willi and A. Grundhöfer, “Robust Geometric Self-Calibration of Generic Multi-Projector Camera Systems,” In Proceedings of IEEE International Symposium on Mixed and Augmented Reality (ISMAR), pp. 42-51, 2017.

5. Noah Snavely, Steven M. Seitz, and Richard Szeliski, “Modeling the World from Internet Photo Collections,” International Journal of Computer Vision, Vol. 80, No. 2, pp. 189-210, 2008.

#1「プロジェクションマッピング作品を通して見る技術課題」
１　建築物へのプロジェクションマッピング
２　インタラクティブなプロジェクションマッピング
３　動的プロジェクションマッピング
４　まとめ

#2「プロジェクションマッピングの多様なアプリケーション」
１　照明の知能化
１．１　リビング照明の知能化
１．２　作業空間の照明の知能化
２　表面質感の編集
３　まとめ

#3 「幾何補正 (位置合わせ)」
１　平面を対象とする場合の幾何補正
２　立体面を対象とする場合の幾何補正
２．１　対象面形状が既知の場合の較正
２．２　対象面形状が未知の場合の較正
２．２．１　事前プロカム較正アプローチ
２．２．２　事前カメラ較正アプローチ
２．２．３　自動較正アプローチ

#4「色補償」
１　準備
２　簡易手法
３　色変換行列手法
４　非線形補間手法
５　ダイナミックレンジ制約の解消法
６　まとめ

#5「複雑な光学現象への対応（１）」
１　相互反射補償
２　焦点ボケ補償
２．１　複数台投影アプローチ
２．２　1台投影アプローチ
２．３　投影光学系の工夫による１台投影における技術的限界の解消
３．まとめ

#6「 複雑な光学現象への対応（２）」
１　表面化散乱補償
２　ライトトランスポート行列を用いた大域照明効果の一括補償
３　おわりに

#7「影の除去」
1　複数台のプロジェクタを用いた影除去
2　光学系の工夫による影除去
3　まとめ

#8「ハイダイナミックレンジ投影」
１　プロジェクタのダイナミックレンジ拡張
１．１　単純に最大照度を上げてもダイナミックレンジは改善しない
１．２　最小照度を下げてダイナミックレンジを拡げる技術
１．３　最大照度向上と最小照度抑制によるダイナミックレンジ拡張技術
２　プロジェクションシステムのダイナミックレンジ拡張